木叶清风,C++,Python,Java,C#,Unity3d,Unreal4,UE4,技术日志

# 3D数学基础

# 向量

向量指具有大小(magnitude)和方向的量，可以表示物体的位置和方向。

# 向量大小

向量的大小是其各分量平方和的平方根。在Unity3d中可以如下操作：

Vector3 v1 = new Vector3(1, 2, 3);
//长度
Debug.Log(v1.magnitude);
//长度的平方，可节省计算性能
Debug.Log(v1.sqrMagnitude);
1
2
3
4
5

# 向量方向

获取向量方向也称为"标准化向量"或"归一化向量"，即获取该向量的单位向量(大小为1的向量)。在Unity3d中如下操作：

Vector3 v1 = new Vector3(1, 2, 3);
Debug.Log(v1.normalized);//返回标准化的结果
Debug.Log(v1);
v1.Normalize();//将v1自身标准化
Debug.Log(v1);
1
2
3
4
5

# 向量加减乘除

向量相减等于各分量相减，向量a减向量b，将以向量b的终点为起始点，以向量a的终点为终点的向量，方向是由b指向a。它常应用于计算两点之间的距离和相对方向。

向量相加等于各分量相加，向量a与向量b相加，平移使b的始点与a的终点重合，结果为以a的始点为始点，以b的终点为终点的向量。它常用于物体移动。

向量与标量乘除是该向量的各分量与标量相乘除。它常用于缩放向量长度。

# 三角函数

角的度量方式，角度(Degree)和弧度(Radian)。在一个圆中，弧长等于半径的弧，其所对的圆心角就是 1rad。也就是说，两条射线从圆心向圆周射出，形成一个夹角和夹角正对的一段弧。当这段弧的长度正好等于圆的半径时，两条射线的夹角的弧度为 1。

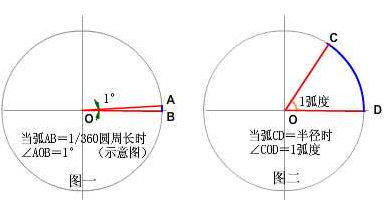
degRad

角度和弧度换算：

PI=180度，1弧度=180度/PI，1角度=PI/180度

Unity3d中常用的三角函数运算：

弧度=角度数*Mathf.Deg2Rad
角度=弧度数*Mathf.Rad2Deg

Mathf.Sin(float radian)
Mathf.Cos(float radian)
Mathf.Tan(float radian)

Mathf.Asin(float radian)
Mathf.Acos(float radian)
Mathf.Atan(float radian)
1
2
3
4
5
6
7
8
9
10

# 向量点乘

向量点积又称点积或内积，是各分量乘积和，它的集合意义是两个向量的单位向量相乘后再乘以二者夹角的余弦值。

a·b=|a| · |b| cos/<a,b/>

对于标准化过的向量，点乘结果等于两向量夹角的余弦值。它常用于计算两向量夹角：

float dot =Vector3.Dot(a.normalized, b.normalized);
float angle = Mathf.Acos(dot) * Mathf.Rad2Deg;
1
2

对于标准化过的向量，方向完全相同，点乘结果为1，完全相反，点乘结果为-1，互相垂直结果为0。

# 向量叉乘

向量叉乘又称为叉积或外积，它的几何意义是为两个向量所组成面的垂直向量，模长为两向量模长乘积再乘夹角的正弦值。

[x1,y1,z1] x [x2,y2,z2] = [y1 * z2 - z1 * y2, z1 * x2 - x1 * z2, x1 * y2 - y1 * x2] a·b=|a| · |b| sin/<a,b/>

它常应用于创建垂直于平面的向量。

Vector3 cross = Vector3.Cross(a.normalized, b.normalized);
float angle = Mathf.Asin(cross.magnitude) * Mathf.Rad2Deg;
1
2

# 常用API

向量在Unity3d主要应用于位置变换，常用API有：

Vector3.Lerp
Vector3.MoveTowards 
Vector3.SmoothDamp
Vector3.Angle
Vector3.ProjectOnPlane
Vector3.Reflect
1
2
3
4
5
6

# 欧拉角

此处内容参考：

欧拉角使用三个角度来保存方位，它包含：pitch(俯仰)，Yaw(偏航)，Roll(桶滚)。

我们可以使用平衡环架(Gimbal)来模拟欧拉角的旋转：

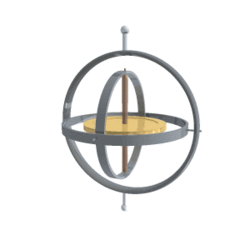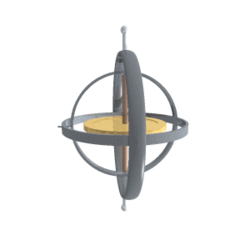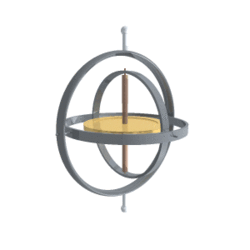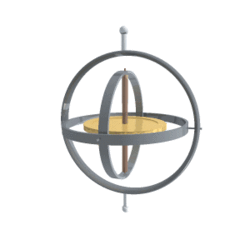
gimbal

平衡环架（英语：Gimbal）为一具有枢纽的装置，使得一物体能以单一轴旋转。由彼此垂直的枢纽轴所组成的一组三只平衡环架，则可使架在最内的环架的物体维持旋转轴不变，而应用在船上的陀螺仪、罗盘、饮料杯架等用途上，而不受船体因波浪上下震动、船身转向的影响。在载体高速转动的时候，平衡环架始终要通过自我调节，使得里面转子保持原有的平衡。

在进行Roll(桶滚)时：

roll

进行pitch(俯仰)时：

pitch

进行Yaw(偏航)时：

yaw

主要欧拉角是有顺序的，Unity3d中旋转顺序是y->x->z，旋转y轴，x和z都变，旋转x轴，只有z轴变化，旋转z轴，其他轴不变。

它的优点是：

  • 仅使用三个数字表达方位，占用空间小。
  • 沿坐标轴旋转的单位为角度，符合人的思考方式。
  • 任意三个数字都是合法的，不存在不合法的欧拉角。

它的缺点是，对于一个方位，有多个欧拉角描述，无法判断多个欧拉角代表的角位移是否相同，比如角度0,5,0与角度0,365,0。

为了保证任意方位都只有独一无二的表示，Unity引擎限制了角度范围，即沿X轴旋转限制在-90到90之间，沿Y与Z轴旋转限制在0到360之间。

Vector3 eulerAngle = this.transform.eulerAngles;

# 万向节死锁

物体沿X轴旋转±90度，自身坐标系Z轴与世界坐标系Y轴将重合，此时再沿Y或Z轴旋转时，将失去一个自由度。在万向节死锁情况下，规定沿Y轴完成绕竖直轴的全部旋转，即此时Z轴旋转为0。

用上面的模型来描述万向节死锁就是：

lock

# 四元数

Quaternion 在3D图形学中代表旋转，由一个三维向量(X,Y,Z)和一个标量(W)组成。

旋转轴为X，旋转弧度为θ，如果使用四元数表示，则四个分量为：

  • x=sin(θ /2)*V.x
  • y=sin(θ /2)*V.y
  • z=sin(θ /2)*V.z
  • w=cos(θ /2)

X、Y、Z、W的取值范围是-1到1。Unity3d中获取四元数：

Quaternion qt = this.transform.rotation;

# 四元数运算

四元数左乘向量，表示将该向量按照四元数表示的角度旋转：

Vector3 point = new Vector3(0,0,10);
Vector3 newPoint = Quaternion.Euler(0,30,0) * point ;
1
2

两个四元数相乘可以组合旋转效果，下面两个旋转效果是一样的：

Quaternion rotation01 = Quaternion.Euler(0, 30, 0) * Quaternion.Euler(0, 20, 0);
Quaternion rotation02 = Quaternion.Euler(0, 50, 0);
1
2

四元数的优点是能避免万向节死锁：

this.transform.rotation *= Quaternion.Euler(0, 1, 0); //可使物体沿自身坐标Y轴旋转
this.transform.Rotate(Vector3 eulerAngles) //内部就是使用四元数相乘实现
1
2

它的缺点是：难以使用，不直观，不建议单独修改某个数值。

# 常用接口

四元数常用于角度旋转，它的API有：

Quaternion.LookRotation
Quaternion.Euler
Quaternion.Lerp
Quaternion.FromToRotation
Quaternion.AngleAxis
1
2
3
4
5

←